DeepSeek-AI’s new framework solves the instability of Hyper-Connections, paving the way for scalable, next-gen foundation models.
- The Scalability Bottleneck: While recent Hyper-Connections (HC) have boosted AI performance by expanding network width, they fundamentally break the “identity mapping” property, leading to severe training instability and memory overheads in large models.
- The Mathematical Fix: DeepSeek-AI introduces Manifold-Constrained Hyper-Connections (mHC), a framework that uses the Sinkhorn-Knopp algorithm to project connections onto a specific manifold, ensuring signals remain stable and energy is conserved.
- Future-Proofing AI: Empirical tests show mHC restores stability and scalability without adding computational cost, reigniting interest in topological architecture design for the next generation of foundational models.
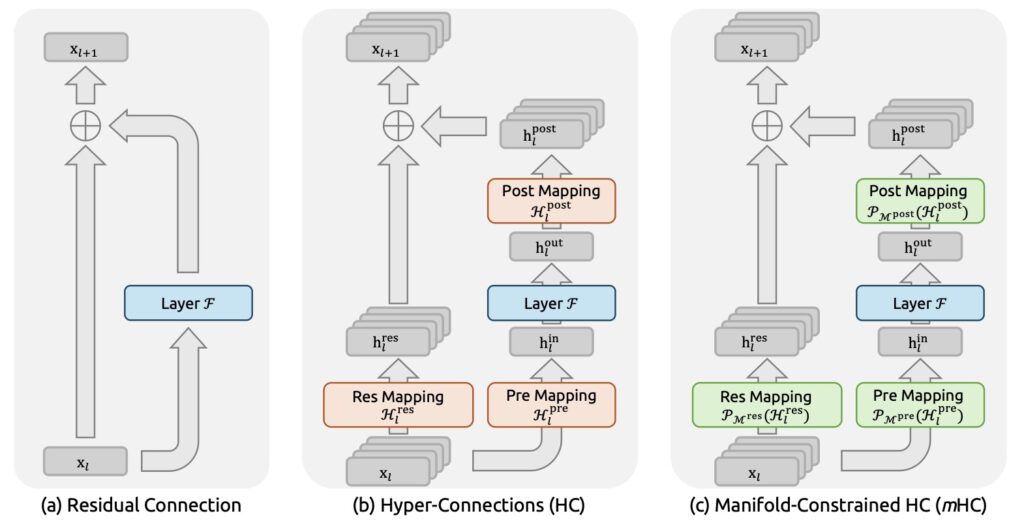
For the past decade, the landscape of deep learning has been dominated by a single, powerful paradigm: the residual connection. This architectural backbone allowed neural networks to go deeper than ever before. However, the relentless pursuit of more powerful foundational models has pushed researchers to look beyond the standard residual stream.
Recently, Hyper-Connections (HC) emerged as a promising evolution. By expanding the width of the residual stream and diversifying how layers connect, HCs yielded substantial performance gains. Yet, this innovation came at a steep cost. In this article, we explore how DeepSeek-AI’s new proposal, Manifold-Constrained Hyper-Connections (mHC), addresses the fatal flaws of HC to create a robust framework for the future of AI.
The Double-Edged Sword of Hyper-Connections
To understand the innovation of mHC, we must first understand the problem it solves. Standard Hyper-Connections attempt to improve learning by creating a denser, more complex web of connections between layers. While this looks good on paper, the unconstrained nature of these connections creates a “wild west” environment for data signals.
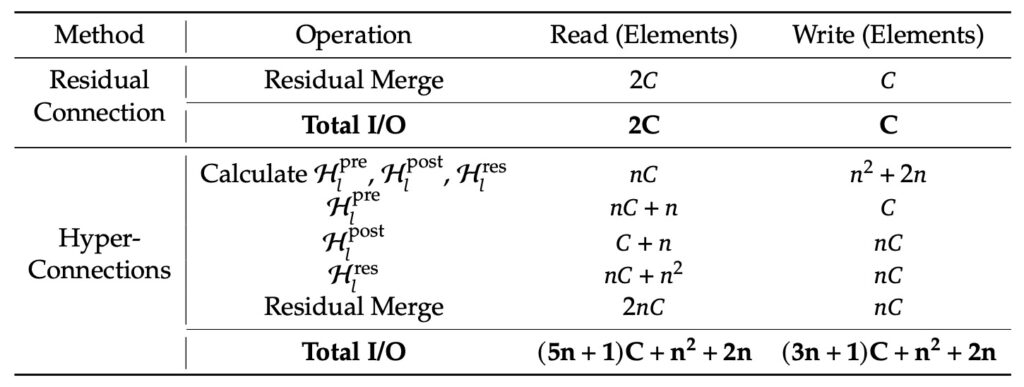
DeepSeek-AI identifies that this diversification fundamentally compromises the identity mapping property—the safety mechanism intrinsic to residual connections that allows signals to pass through unchanged if necessary. Without this constraint, HC leads to signal divergence. As data moves through the deep network, the signal energy is not conserved; it becomes disrupted and chaotic. This results in severe training instability, causing models to fail to converge, and restricts the ability to scale these architectures up to the massive sizes required for modern AI. Furthermore, the sheer volume of unconstrained connections incurs notable memory access overhead.
Restoring Order: The mHC Solution
DeepSeek-AI’s solution is not to abandon Hyper-Connections, but to tame them. They propose Manifold-Constrained Hyper-Connections (mHC). This framework accepts the expanded width and diversity of HC but forces the connections to adhere to strict mathematical rules.
Think of it as adding traffic lanes to a highway (HC) but installing intelligent traffic lights to prevent gridlock (mHC).
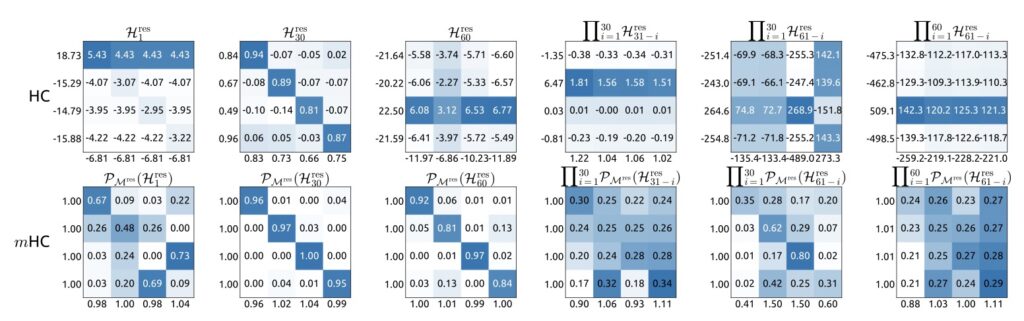
Technically, mHC projects the chaotic residual connection space onto a specific manifold to restore the identity mapping property. To achieve this, the researchers employ the Sinkhorn-Knopp algorithm. This algorithm enforces a “doubly stochastic constraint” on the residual mappings. In simpler terms, it balances the flow of information so that signal propagation becomes a “convex combination” of features. This ensures that the signal energy is conserved across layers, preventing the divergence that plagued the original HC approach.
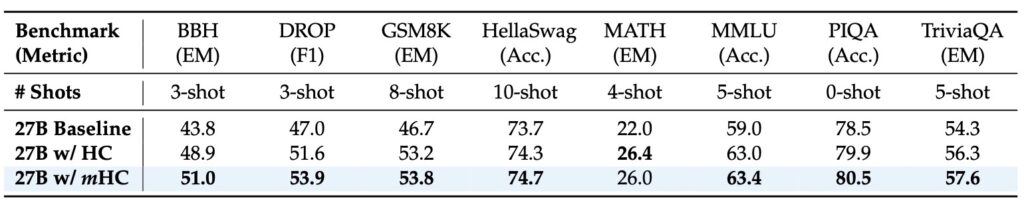
Efficiency Without Compromise
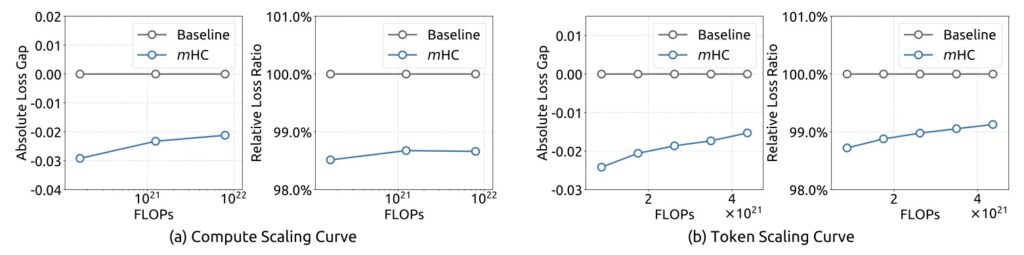
One of the most impressive aspects of the mHC framework is its practicality. Theoretical improvements often come with heavy computational taxes, but mHC is designed with rigorous infrastructure optimization in mind.
Empirical experiments demonstrate that mHC is highly effective for training at scale. It offers the tangible performance improvements promised by Hyper-Connections but with superior scalability and stability. Crucially, because of the infrastructure-level optimizations, mHC delivers these benefits with negligible computational overhead. It provides the best of both worlds: the plasticity and learning capability of Hyper-Connections with the stability and efficiency of traditional residual networks.
Rejuvenating Macro-Architecture Design
The implications of mHC extend far beyond a single technical fix. This work signals a potential renaissance in macro-architecture design. By proving that topological structures can be mathematically constrained to optimize the trade-off between plasticity (learning) and stability, DeepSeek-AI opens new avenues for research.
While the current mHC framework utilizes doubly stochastic matrices, the architecture is flexible enough to accommodate diverse manifold constraints tailored to specific learning objectives. This flexibility suggests that we are only scratching the surface of what topological optimization can achieve. As we look toward the next generation of foundational architectures, mHC stands as a critical step forward, illuminating how geometric constraints can tame complexity and drive the evolution of deep learning.