Mastering undergraduate and graduate-level theorems through experience-based learning and efficient scaling.
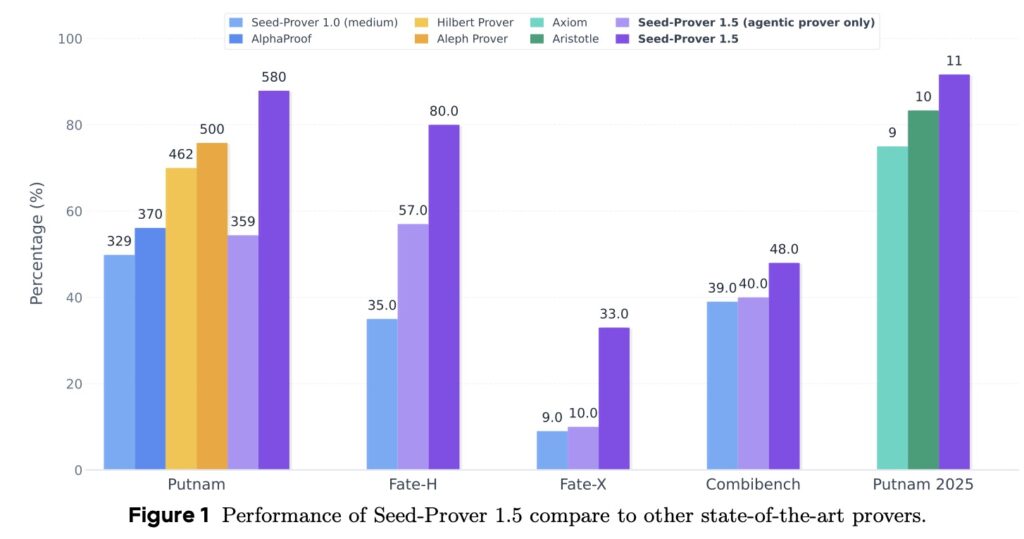
- Unmatched Efficiency and Accuracy: Seed-Prover 1.5 outperforms state-of-the-art models with a fraction of the compute budget, solving 88% of undergraduate-level PutnamBench problems and 11 out of 12 problems from the 2025 Putnam competition.
- Bridging Two Worlds: The system utilizes a novel workflow that connects natural language reasoning with formal code (Lean), effectively eliminating hallucinations and ensuring trustworthy verification.
- The Path to Frontier Research: While currently dominant in competition math, the model lays the groundwork for tackling open mathematical conjectures by addressing the “dependency issue” in future iterations.
The landscape of artificial intelligence is currently witnessing a fierce battle for supremacy in mathematical reasoning. While Large Language Models (LLMs) have demonstrated an impressive ability to generate natural language proofs, a critical divide remains. On one side, we have natural language models that are accessible but prone to logical errors and “hallucinations.” On the other, we have formal theorem proving (using languages like Lean) which offers fully trustworthy verification but has historically been computationally expensive and difficult to scale.
Enter Seed-Prover 1.5, a formal theorem-proving model that promises to close this gap. By leveraging large-scale agentic reinforcement learning (RL) and an efficient test-time scaling (TTS) workflow, this new system is redefining what is possible in automated mathematics.
The Challenge: Rigor vs. Efficiency
To understand the breakthrough of Seed-Prover 1.5, one must first understand the current dilemma in AI mathematics. Formal verification is widely regarded as a paradigm shift for research because it guarantees correctness. However, it comes with a heavy “performance tax.”
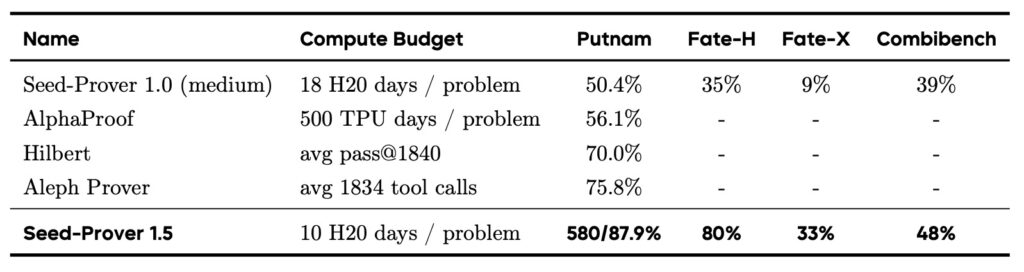
For instance, previous heavyweights like AlphaProof solved 56% of the full Putnam benchmark but required massive resources—approximately 500 TPU-days per problem. Conversely, natural language models like DeepSeek-Math-V2achieved near-perfect scores on the Putnam 2024 competition but lacked the rigorous, verify-first architecture of formal languages. This led to a pressing question: Is pursuing formal theorem proving still a viable path if natural language models are so capable?
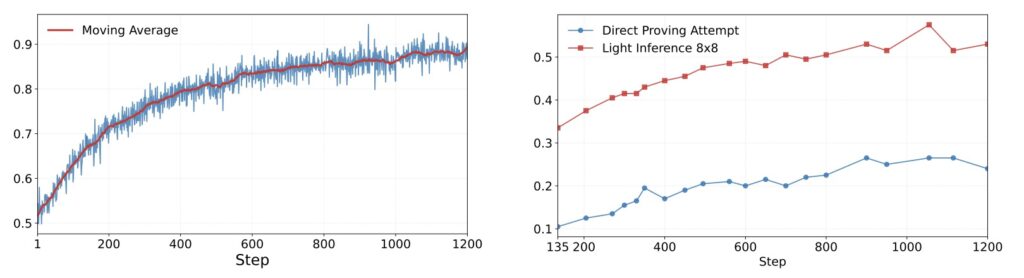
Seed-Prover 1.5 answers with a resounding “yes.” It demonstrates that formal proving does not have to be inefficient. By continuously accumulating experience through interactions with Lean and other tools during its training process, the model has substantially enhanced both its capability and efficiency.
Shattering Records with Less Compute
The performance metrics of Seed-Prover 1.5 are nothing short of startling. It achieves superior performance compared to state-of-the-art methods while utilizing a significantly smaller compute budget.
The model’s proficiency spans several levels of mathematical difficulty:
- Undergraduate Level: Solves 88% of PutnamBench.
- Graduate Level: Solves 80% of Fate-H.
- PhD Level: Solves 33% of Fate-X.
Perhaps most impressively, when put to the test against the most recent standards, the system solved 11 out of 12 problems from the Putnam 2025 competition within just 9 hours. This level of speed and accuracy suggests that scaling learning from experience, driven by high-quality formal feedback, is the key to the future of formal mathematical reasoning.
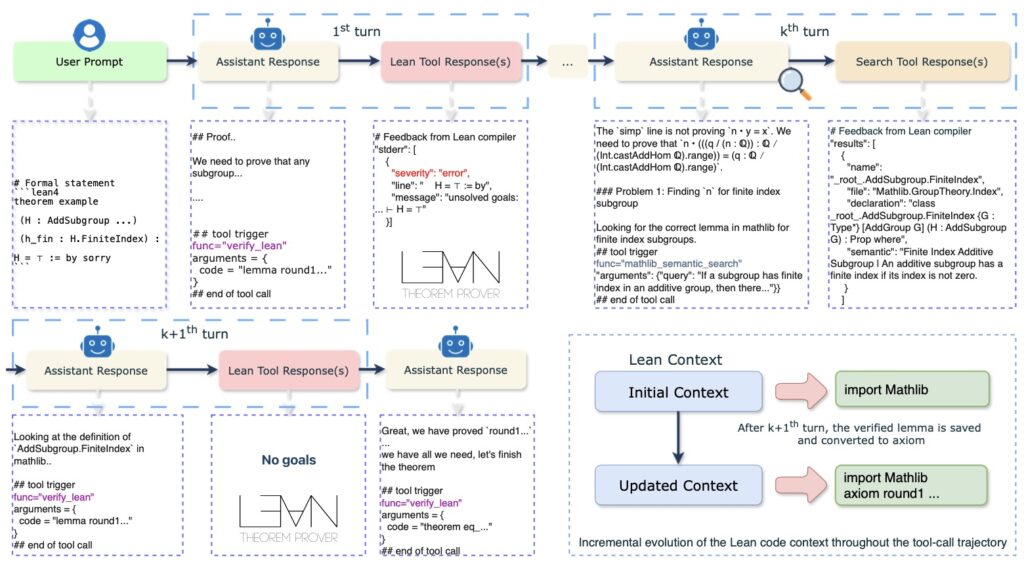
The Workflow: Bridging Natural and Formal Languages
How does Seed-Prover 1.5 achieve this balance? The secret lies in its architecture. It functions as a high-performance agentic Lean prover integrated with a sketch model.
This sketch model serves as a bridge between the intuitive, flexible nature of natural language and the rigid, rigorous structure of formal Lean code. By leveraging recent advancements in natural language proving, the TTS workflow efficiently translates mathematical intuition into verifiable code. This eliminates the logical errors pervasive in natural language proofs while maintaining the creativity required to solve complex problems.
The Next Frontier: Overcoming the Dependency Issue
Despite these triumphs, the creators of Seed-Prover 1.5 acknowledge that the system cannot yet make significant mathematical contributions comparable to human experts in “frontier” research. This limitation stems from the “dependency issue.”
Competition problems, such as those in the IMO or Putnam, are self-contained; they do not require knowledge of specific prior research papers. However, driving progress in real-world mathematics typically hinges on synthesizing insights across a multitude of related academic papers.
To move from solving competitions to resolving open mathematical conjectures, future iterations must address three challenges:
- Identifying the most influential and relevant papers.
- Conducting natural language proofs grounded in these specific works.
- Developing scalable approaches to formalize both the papers and the results derived from them.
Seed-Prover 1.5 has laid a solid foundation. By mastering the translation of intuition into formal proof, it has brought us one step closer to an era where AI doesn’t just solve puzzles, but actively participates in the discovery of new mathematics.
